Compounding interest is when you earn interest not only on your principal (the $100) but also on the interest that you already earned. So after year 2 you are not only earning interest on your original $100 investment but also the $10 of interest that you earned after year 1. Now $1 may not seem like a lot, but things add up quickly.
Let me show you a real-life example. Say you graduate from college, and you start earning your first paycheck when you turn 22. At age 22, you start putting $300 a month into a Roth IRA (a type of retirement fund where you put money in after you paid taxes on that money). That brings your yearly contribution to $3,600. Lets further assume that you contribute $300 every month to your Roth IRA through your 30th birthday and then don't contribute any more money to your IRA for the rest of your life. If your investment earns an annual return of 10% (the average annual return of the stock market over time), how much would you have by the time you retired at age 65? Any guesses?
Maybe a few hundred thousand? You may think $200,000 would be a nice chunk of change that would be waiting for you at 65 after you only put in $32,400 total. Well I think you will be pleasantly surprised....... drum roll........$1.37 million! You could be a millionaire when you retire! Don't believe me? Here is the year by year breakdown of what you put in each year and your total at the end of the year:
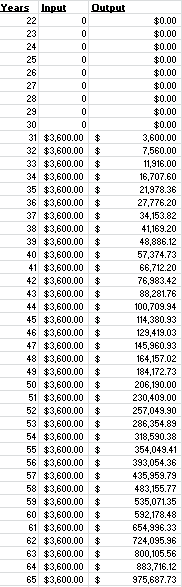
You can see that at the beginning, say the first 10 years after you stopped saving, your investment does not grow that large. This is because compounded interest needs time to work. The sooner you start saving the better! Let me show you another example that illustrates the importance of saving as early as possible. In this example, you start saving $300 a month when you turn 31 and continue to save $300 a month every month until you retire at age 65 (a total contribution of $126,000). If you earn 10% annually, how much money do you think you would have at 65? It has to be more than $1.37 million right? Maybe $4 million? $8 million. Let your imagination go......drum roll......$975,000. That's right. Less than a million dollars. Less than the first example! Here is proof:
The point is, start saving early because it does not make much initial money to make you a millionaire! Of course, compounding interest can also work against you if you have debt, so it's important that you pay off your debt as quick as you can. If you would like me to crunch some number for your unique situation, let me know!
Take care.
Maybe a few hundred thousand? You may think $200,000 would be a nice chunk of change that would be waiting for you at 65 after you only put in $32,400 total. Well I think you will be pleasantly surprised....... drum roll........$1.37 million! You could be a millionaire when you retire! Don't believe me? Here is the year by year breakdown of what you put in each year and your total at the end of the year:
You can see that at the beginning, say the first 10 years after you stopped saving, your investment does not grow that large. This is because compounded interest needs time to work. The sooner you start saving the better! Let me show you another example that illustrates the importance of saving as early as possible. In this example, you start saving $300 a month when you turn 31 and continue to save $300 a month every month until you retire at age 65 (a total contribution of $126,000). If you earn 10% annually, how much money do you think you would have at 65? It has to be more than $1.37 million right? Maybe $4 million? $8 million. Let your imagination go......drum roll......$975,000. That's right. Less than a million dollars. Less than the first example! Here is proof:
The point is, start saving early because it does not make much initial money to make you a millionaire! Of course, compounding interest can also work against you if you have debt, so it's important that you pay off your debt as quick as you can. If you would like me to crunch some number for your unique situation, let me know!
Take care.

No comments:
Post a Comment